Data-Mining

Cours-TP sur la validation des méthodes d'apprentissage

Description du TP
Les données
SVM
Paramètres
Affichage de la matrice de confusion
Validation croisée
Choix des paramètres à tester
SVM

Description du TP

Le but de ce TP est de comprendre et mettre en oeuvre des méthodes de validation utlisée lors de la calibration de méthodes d'apprentissage.

Nous allons comparer les approches naïves aux approches de validation croisée et de leave-one-out.

function CoursTP_VC_ROC()

clear all;
close all;

Les données

Nous allons utiliser des données synthétiques, aussi appelées données jouet, dans un but d'illustration.

nombre de points en apprentissage

N = 50;

nombre de points en test

Ntest = 1000;

génération et mélange des données

x1 = [0.3*randn(round(N/2),2)+0.3;0.35*randn(round(N/2),2)-0.2];
y1 = [ones(round(N/2),1);-ones(round(N/2),1)];
temp = randperm(length(y1));
x1 = x1(temp,:);
y1 = y1(temp);
xtest1 = [0.3*randn(round(Ntest/2),2)+0.3;0.35*randn(round(Ntest/2),2)-0.2];
ytest1 = [ones(round(Ntest/2),1);-ones(round(Ntest/2),1)];

On a besoin de savoir quelle est la première classe rencontrée par l'algorithme d'apprentissage

c1 = y1(1);
c2 = -c1;

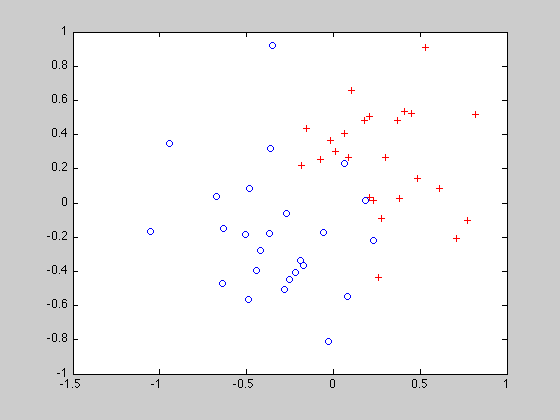
Visualisation

figure;
plot(x1(y1==1,1),x1(y1==1,2),'r+');
hold on;
plot(x1(y1==-1,1),x1(y1==-1,2),'bo');

SVM

La méthode d'apprentissage que nous allons utiliser pour ce TP est appelée SVM (Séparateurs à Vaste Marge). Cette méthode permet de faire de la discrimination et requière le réglage de plusieurs paramètres. Sans rentrer dans les détails, nous allons ici nous intéresser au réglage de 2 paramètres, nommés respectivement 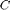$C$ et $\gamma$ .

La toolbox est disponible là et les instruction pour pouvoir l'utiliser sont là Tout d'abord, il faut ajouter le chemin jusqu'aux exécutables du SVM

addpath('../Toolbox/libsvm-mat-2.88-1/');

Paramètres

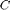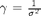le paramètre $C$ prend une valeur réelle strictement positive. Habituellement, l'ordre de grandeur varie entre 1 et 10000. le paramètre $\gamma$ est également un réel strictement positif et est lié à une notion d'écart-type : $\gamma = \frac{1}{\sigma^2}$ .

Prennons deux valeurs, correspondant d'une part à une faible tolérance aux erreurs d'apprentissage (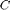 $C$ grand) et d'autre part à une très faible largeur de bande ( $\gamma$ grand), soit une faible influence de chaque point dans la solution.

C = 1000;
gamma = 100;
param = ['-b 1 -c ', num2str(C), ' -g ', num2str(gamma)];

Lançons l'apprentissage

model = svmtrain(y1, x1, param);

Testons la performance du modèle sur les données d'apprentissage

disp('Performance en apprentissage');
[p] = svmpredict(y1, x1, model);

Performance en apprentissage
Model supports probability estimates, but disabled in predicton.
Accuracy = 100% (50/50) (classification)

Puis testons sur des données de test et affichons la décision rendue par le SVM sur tout l'espace.

disp('Performance en test');
[predict_label, accuracy, proba] = svmpredict(ytest1, xtest1, model, '-b 1');

Performance en test
Accuracy = 74.5% (745/1000) (classification)

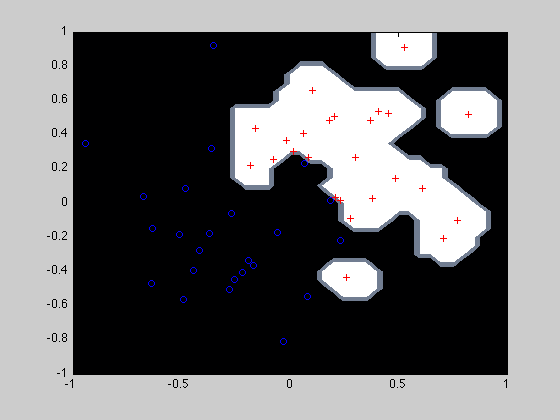
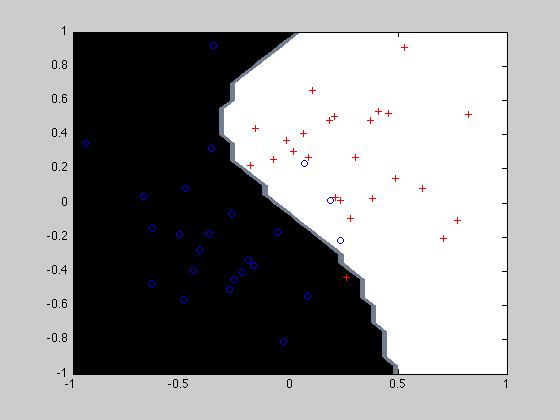
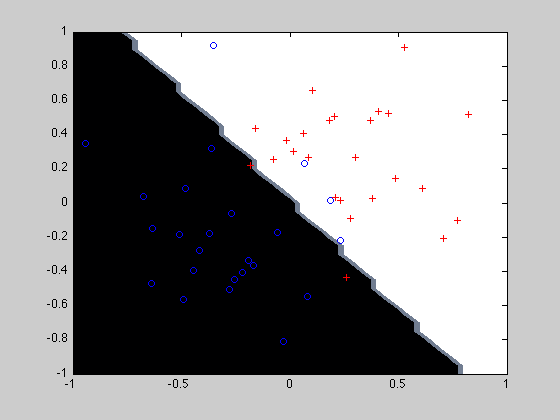
Affichage du SVM Le code de l'affichage se trouve là

afficherSVM(model, x1,y1);

------------------------------------
Les valeurs affichées ci-dessous n'ont pas de sens car les étiquettes sont absentes...
Model supports probability estimates, but disabled in predicton.
Accuracy = 0% (0/1681) (classification)
------------------------------------

Affichage de la matrice de confusion

Le code de la matrice de confusion se trouve là

MCBase = matriceConfusion(ytest1,predict_label,c1,c2)

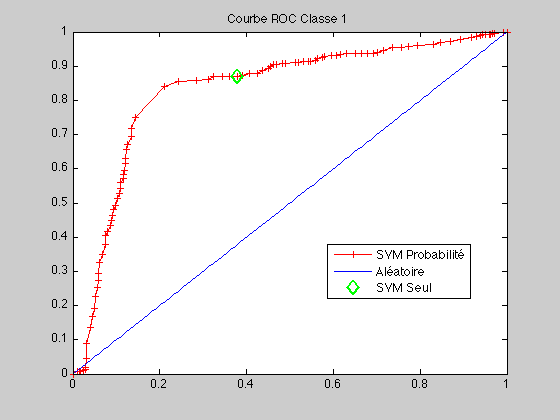
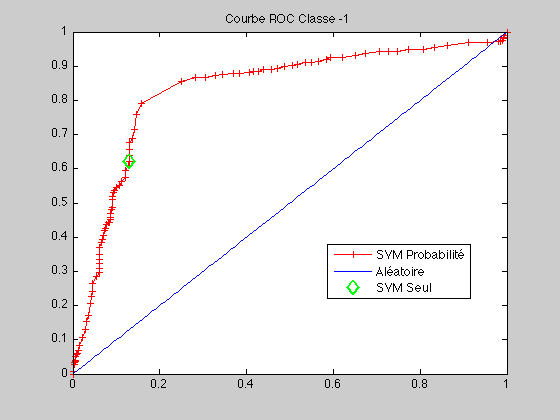
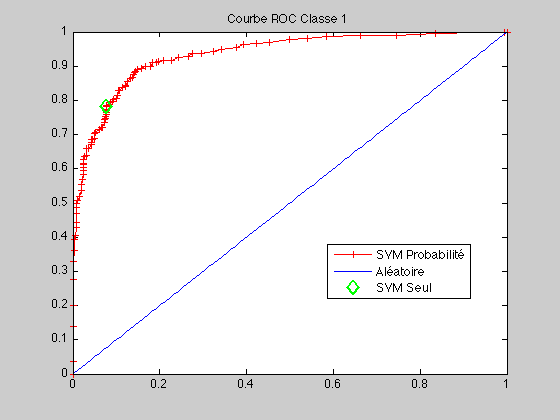
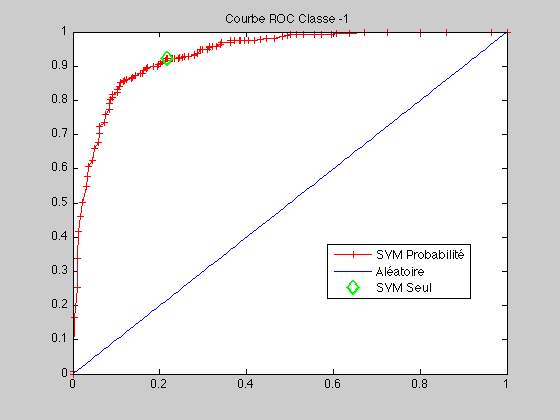
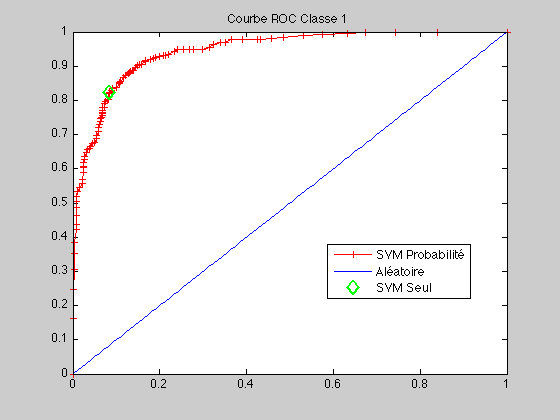
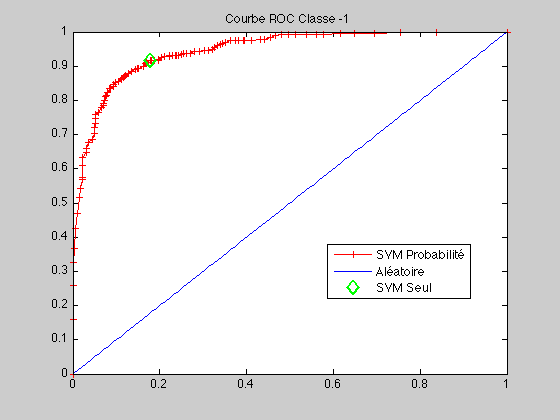
Etudions la courbe ROC Le code de la courbe ROC se trouve là

courbeROC(c1,c2,ytest1,proba,predict_label)

Prennons deux autres valeurs

C = 10;
gamma = 1;
param = ['-b 1 -c ', num2str(C), ' -g ', num2str(gamma)];
model = svmtrain(y1, x1, param);
disp('Performance en apprentissage');
[p] = svmpredict(y1, x1, model);
disp('Performance en test');
[predict_label, accuracy, proba] = svmpredict(ytest1, xtest1, model, '-b 1');
afficherSVM(model, x1,y1);
MCBase = matriceConfusion(ytest1,predict_label,c1,c2)
courbeROC(c1,c2,ytest1,proba,predict_label);

Performance en apprentissage
Model supports probability estimates, but disabled in predicton.
Accuracy = 92% (46/50) (classification)
Performance en test
Accuracy = 85.2% (852/1000) (classification)
------------------------------------
Les valeurs affichées ci-dessous n'ont pas de sens car les étiquettes sont absentes...
Model supports probability estimates, but disabled in predicton.
Accuracy = 0% (0/1681) (classification)
------------------------------------

MCBase =

   461    39
   109   391

Validation croisée

La validation croisée permet de vérifier la pertinence d'un ensemble de tuples de paramètres sans utiliser les données de test, en utilisant un découpage de la base d'apprentissage en $N$ morceaux. Chaque morceau sert une fois de jeu de validation pendant que le complément sert de base d'apprentissage. La performance d'un tuple de paramètre est évalué par moyennage (voir code de la validation croisée qui se trouve là)

Choix des paramètres à tester

Choisir le nombre de découpages pour la validation croisée, la liste de
valeurs de paramètres à tester, et effectuer cette validation.

nbFolders = 3;
C = [1 10 100 1000 10000];
bandwidth = [0.01 0.1  1  10];
 [I,J] = crossValidationClassBin(x1,y1,nbFolders,C,bandwidth);

Accuracy = 41.1765% (7/17) (classification)
Accuracy = 94.1176% (16/17) (classification)
Accuracy = 94.1176% (16/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 94.1176% (16/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 94.1176% (16/17) (classification)
Accuracy = 94.1176% (16/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 88.2353% (15/17) (classification)
Accuracy = 47.0588% (8/17) (classification)
Accuracy = 76.4706% (13/17) (classification)
Accuracy = 76.4706% (13/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 76.4706% (13/17) (classification)
Accuracy = 76.4706% (13/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 70.5882% (12/17) (classification)
Accuracy = 76.4706% (13/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 70.5882% (12/17) (classification)
Accuracy = 82.3529% (14/17) (classification)
Accuracy = 76.4706% (13/17) (classification)
Accuracy = 70.5882% (12/17) (classification)
Accuracy = 70.5882% (12/17) (classification)
Accuracy = 76.4706% (13/17) (classification)
Accuracy = 64.7059% (11/17) (classification)
Accuracy = 70.5882% (12/17) (classification)
Accuracy = 70.5882% (12/17) (classification)
Accuracy = 43.75% (7/16) (classification)
Accuracy = 93.75% (15/16) (classification)
Accuracy = 87.5% (14/16) (classification)
Accuracy = 87.5% (14/16) (classification)
Accuracy = 93.75% (15/16) (classification)
Accuracy = 93.75% (15/16) (classification)
Accuracy = 87.5% (14/16) (classification)
Accuracy = 75% (12/16) (classification)
Accuracy = 93.75% (15/16) (classification)
Accuracy = 93.75% (15/16) (classification)
Accuracy = 87.5% (14/16) (classification)
Accuracy = 75% (12/16) (classification)
Accuracy = 93.75% (15/16) (classification)
Accuracy = 93.75% (15/16) (classification)
Accuracy = 81.25% (13/16) (classification)
Accuracy = 75% (12/16) (classification)
Accuracy = 93.75% (15/16) (classification)
Accuracy = 87.5% (14/16) (classification)
Accuracy = 81.25% (13/16) (classification)
Accuracy = 75% (12/16) (classification)

SVM

Lancer l'apprentissage final avec les paramètres issus de la validation croiée

bestGs = bandwidth(J(1))
bestCs = C(I(1))
param = ['-b 1 -c ', num2str(bestCs), ' -g ', num2str(bestGs)];
model = svmtrain(y1, x1, param);
disp('Performance en apprentissage');
[p] = svmpredict(y1, x1, model);
disp('Performance en test');
[predict_label, accuracy, proba] = svmpredict(ytest1, xtest1, model, '-b 1');
afficherSVM(model, x1,y1);
MCBase = matriceConfusion(ytest1,predict_label,c1,c2)
courbeROC(c1,c2,ytest1,proba,predict_label);

bestGs =

    0.0100


bestCs =

    10

Performance en apprentissage
Model supports probability estimates, but disabled in predicton.
Accuracy = 88% (44/50) (classification)
Performance en test
Accuracy = 86.9% (869/1000) (classification)
------------------------------------
Les valeurs affichées ci-dessous n'ont pas de sens car les étiquettes sont absentes...
Model supports probability estimates, but disabled in predicton.
Accuracy = 0% (0/1681) (classification)
------------------------------------

MCBase =

   458    42
    89   411

end