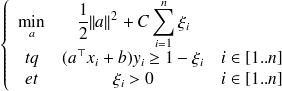Séparateurs à Vaste Marge Linéaire
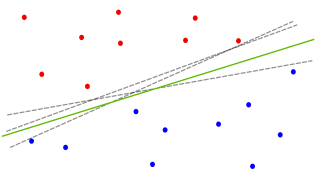
On s'intéresse dans un premier temps au cas de deux classes linéairement séparables, c'est-à-dire qu'il existe au moins une droite (en général, une infinité) expliquant la totalité des données. Dans ce contexte, on se pose la question de trouver la meilleure droite, qui sera définie comme celle qui aura le meilleur pouvoir de généralisation.
Le principe des vastes marges permet d'ajouter des contraintes sur la définition de la droite de telle façon que la solution du problème devient unique. Intuitivement, cela consiste à dire que la meilleure droite parmi toutes celles qui séparent les deux classes est celle qui se trouve le plus loin possible de tous les exemples d'apprentissage (ou encore "au milieu").
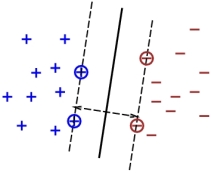
Dans les méthodes à vaste marge, on recherche parmi tous les hyperplans discriminants celui qui maximise la marge, c'est-à-dire celui qui se trouve à égale distance des deux classes à séparer. Cette marge se calcule par rapport au points les plus proches de l'hyper plan, ils sont appelés points supports.
L'hyperplan recherché est alors défini par une fonction
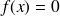telle que
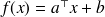et telle que les points support
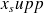répondent à la contrainte
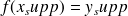(donc
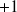ou
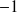en fonction de leur classe). Ainsi, on demande à ce que tous les points d'apprentissage se trouve à une distance minimum de
de la frontière. Plus formellement, on pose le système à résoudre (problème quadratique donc la solution est unique si elle existe) :
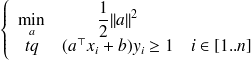
Dans le cas dit non séparable, on introduit une variable de relâchement des contraintes qui permet de tolérer les écarts. En pratique, cela revient à admettre que certains points se trouvent du mauvais côté de leur marge, mais au prix d'une constante
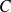qui pénalise la minimisation (cette constante devient un paramètre de la méthode). Le système quadratique à résoudre devient alors :
